复介电常数

复介电常数

在具有介电作用的同时，岩石也具有导电作用。结果就像电容器漏电一样，除了位移电流，还存在传导电流，造成损耗，电流与电压的相位差不再是90°，而要小一些。这一现象可通过一个电容器来解释和研究。

首先考虑一个极板间为真空的电容器（图4－13a），电容量为C0，当两极板间加上交频率为ω的正弦波交变电压时，流过电容器的电流为

储层岩石物理学

储层岩石物理学

其中虚数单位 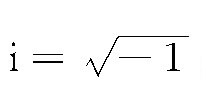，表示I与V有90°的相位差如图4－13b所示。在电容器两极板间填充以相对介电常数为ε的电介质（图4－13c），则电容量将增大到C＝εC0，而通过填充有电解质的电容器的电流则变成

储层岩石物理学

储层岩石物理学

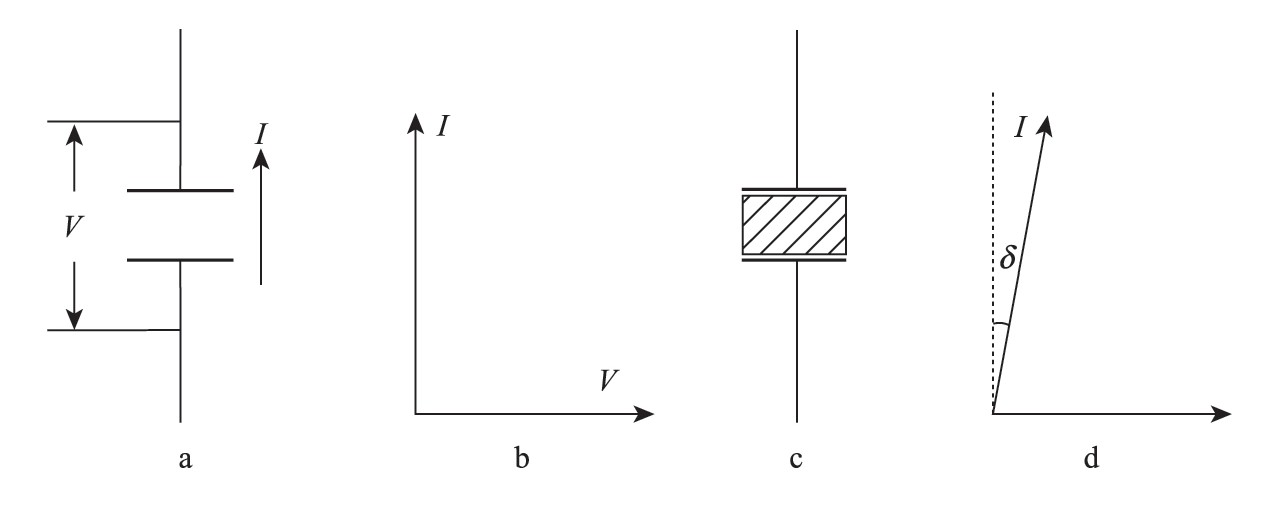
图4－13 岩石的电容等效

图4－13 岩石的电容等效

因为实际的电介质都有损耗，这时观察到的电流I与电压V的相位差总是略小于90°，如图4－13d所示。此处，我们取电压V沿实轴方向，将实验观察到的电流I的实轴分量写为ωε″C0V，而把I的虚轴分量写为iωε′C0V关系，其中ε′和ε″均为实数。于是 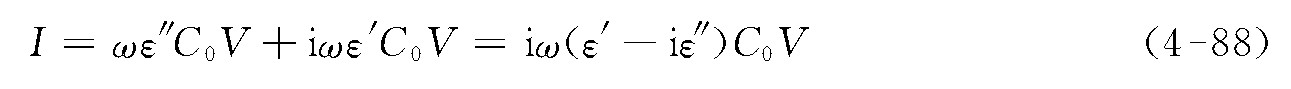与式（4－87）比较，可以得到

储层岩石物理学

储层岩石物理学

也就是说，只要将相对介电常数定义为复数，就能描述在实验中观察到的现象。称ε′为复相对介电常数的实部，ε″为虚部。注意式（4－89）与一般复数表达式的区别，这里虚部采用负号而不是正号，这样做是为了使实际观察到的ε″一般均为正值。

在电路技术中，一个实际的充满电解质的电容器在电路中的表现可以用等效电路来描述。最简单的等效电路就是一个电阻与一个电容的串联或并联，只要他们的阻抗与实际的电容器是一致的（电阻和容抗）。

在一块电介质两端施加交变电压U（ω），则会产生电流I（ω），它们的比值z（ω）＝U（ω）/I（ω）称阻抗，而其倒数y（ω）＝I（ω）/U（ω）称导纳，它们与频率的关系取决于I（ω）。为此，这里我们用理想的电路元件，即其值不随频率变化的电容C、电导G、电阻R和电感L组成各种等效电路，使得等效电路在交变电场作用下的频率响应，与实际电介质在交变电场作用下的效果一致。从而通过等效电路来描述电介质内部的物理过程。这里也可以像第四章第一节第四部分中那样按照串联、并联以及混联等效电路研究复介电常数与阻抗和电容的关系，其做法是类似的。这里只给出并联等效电路的结果：

储层岩石物理学

储层岩石物理学

式中：Cp为并联等效电路的电容；Rp为该等效电路的电阻。阻容串联等效电路与并联电路参数之间存在如下的关系：

储层岩石物理学

储层岩石物理学

式中：Cs为串联等效电路的电容；Rs为该等效电路的电阻。损耗引起的相移角正切为

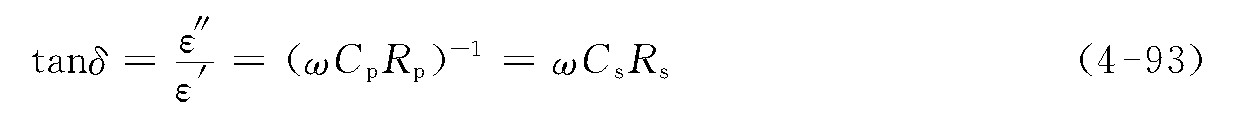
储层岩石物理学

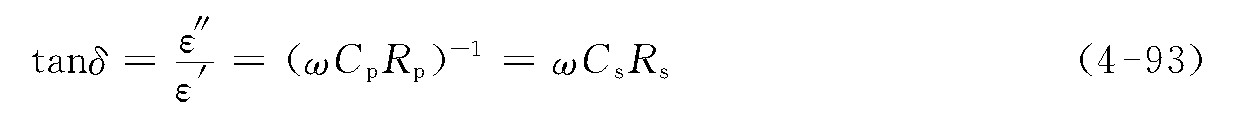
储层岩石物理学

称δ为损耗角，当损耗不大时，δ就等于ε″与ε′的比。