根号3等于多少,怎样手算?要过程 谢谢
的有关信息介绍如下:√3≈1.732
√3是一个无理数,它的小数部分是无限不循环的,无论算多久也算不出小数部分的规律。但是√3不一定只能用计算器算出结果,它的大致结果也能通过手算算出。具体过程如下:

第一步:因为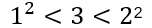
所以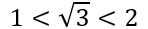 ,因此√3的整数部分是1
,因此√3的整数部分是1
第二步:将区间(1,2)分成两半,一半是(1,1.5),另一半是(1.5,2)
①设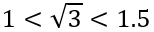 ,则
,则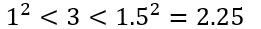 显然不成立
显然不成立
②设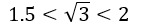 ,则
,则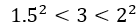 成立,因此
成立,因此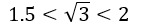
第三步:将区间(1.5,2)分成两半,一半是(1.5,1.75),另一半是(1.75,2)
①设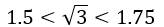 ,则
,则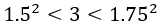 成立。
成立。
②设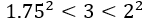 ,则
,则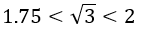 显然不成立,故排除此情况。
显然不成立,故排除此情况。
因此
第四步:将区间(1.5,1.75)分成两半……
第N步:……
由此类推,将区间无限分成两半,√3的值就可无限逼近正确的值。
这个方法类似于函数求零点的二分法。
对于区间[a,b]上连续不断且f(a)·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫二分法。求法如下:
给定精确度ξ,用二分法求函数f(x)零点近似值的步骤如下:
1、确定区间[a,b],验证f(a)·f(b)<0,给定精确度ξ.
2、求区间(a,b)的中点c.
3、计算f(c).
(1) 若f(c)=0,则c就是函数的零点;
(2) 若f(a)·f(c)<0,则令b=c;
(3) 若f(c)·f(b)<0,则令a=c.
(4) 判断是否达到精确度ξ:即若|a-b|<ξ,则得到零点近似值a(或b),否则重复2-4.



